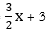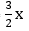Depth of rxy Value: In Case rxy Value = 0.00
Main Article Content
Abstract
If calculating the value of rxy yields 0.00, then X and Y are definitely not linearly correlated. And if these ordered pairs are graphed into rectangular coordinate, they will always look like a symmetrical figure of 1 axis or 2 axes that are parallel to the X axis or the Y axis or both. And if the ordered pairs that are in the same straight line are parallel to only the X axis or Y axis, it will not be able to show how to calculate the rxy value which, by the above principles, must be equal to 0.00. The reason is that when we substitute the values from the ordered pairs that are in the same straight line into the formula of rxy, then the denominator of the formula is 0. So it can be said that it is difficult to explain.
What is more difficult to understand is the general transformation of a two-variable linear equation, Ax + By + C = 0, into a predictive equation, namely y = 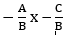
Case 1: If A, B and C ≠ 0, the graph will have a slope such as Ax + By + C = 0 or y = bx + a. Example: -3x + 2y - 6 = 0 or y =
Case 2: If A or B ≠ 0 but C = 0, the graph will have a slope such as Ax + By + 0 = 0 or y = bx. Examples: -3x + 2y = 0 or y =
Case 3: If A or B = 0 and C = 0, the graph which is the X axis (if A = 0) or the Y axis (if B = 0) then has no slope such as (0)x + By + 0 = 0 or y = 0. Examples: (0)x + 5y = 0 or y = 0.
Case 4: If A or B = 0 but C ≠ 0, the graph is parallel to the X or the Y axis, so there is no slope such as (0) x + By + C = 0 or y = (0) x + C. Examples: (0)x - 4y +12 = 0 or y = 3
In case 4, learners are confused and do not understand the reason for the form of these equations because the explanation lacks the use of equation in the form of y = 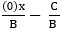
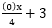
Article Details
The content and information contained in the published article in the Journal of Educational Measurement Mahasarakham University represent the opinions and responsibilities of the authors directly. The editorial board of the journal is not necessarily in agreement with or responsible for any of the content.
The articles, data, content, images, etc. that have been published in the Journal of Educational Measurement Mahasarakham University are copyrighted by the journal. If any individual or organization wishes to reproduce or perform any actions involving the entirety or any part of the content, they must obtain written permission from the Journal of Educational Measurement Mahasarakham University.
References
บุญชม ศรีสะอาด และคณะ. (2555). วิธีการทางสถิติสำหรับการวิจัย. พิมพ์ครั้งที่ 6. มหาสารคาม : คณะศึกษาศาสตร์ มหาวิทยาลัยมหาสารคาม.
สมนึก ภัททิยธนี. (2562). การวัดผลการศึกษา. พิมพ์ครั้งที่ 13. กาฬสินธุ์ : ประสานการพิมพ์.
สมนึก ภัททิยธนี. (2555). คณิตศาสตร์ ชั้นมัธยมศึกษาปีที่ 3. พิมพ์ครั้งที่ 1 กาฬสินธุ์ : ประสานการพิมพ์,
สมนึก ภัททิยธนี. (2559). สิ่งที่น่ารู้เกี่ยวกับ . วารสารการวัดผลการศึกษา มหาวิทยาลัยมหาสารคาม, 22(2), 3–16.